Summary

  1. DiskANN使用64G RAM来索引和服务100维左右的10亿数据集，95%以上的1-recall@1的时延在5ms以内。
  2. 提出Vamana图算法，直径比NSG和HNSW更小。
  3. 将点加入重叠聚类，每个聚类构建Vamana索引，然后通过合并边来实现图合并，和所有数据点构建单一索引的搜索性能相近。

Strength

  1. 通过将点加入重叠聚类，构建的图简单合并也有不错的效果。

Weakness

  1. 图索引用在SSD上，直觉上太多随机访问效果应该会打折扣，虽然Vamana做了优化。后续的SPANN通过层次均衡聚类构建倒排索引，性能超过了DiskANN。
  2. 索引中需要同时存原始向量和PQ压缩向量，应该磁盘使用会比较大。
  3. 性能数据只比较了1-recall@1，很多系统在召回时不止召回一个。

Take Away

图索引合并。

1 引言

总结当前10亿级向量检索的解决方案

方案1。基于倒排索引和数据压缩，典型例子Faiss和IVFOADC+G+P。将向量划分为M个聚类，检索时只扫描m « M个分区；因为原始数据内存中放不下，使用使用PQ等量化手段来压缩数据。优点是内存使用低，128维10亿点使用小于64GB的内存。缺点是由于数据压缩有损，1-recall@1只有0.5左右。

方案2。数据划分为不相交分片，每个分片构建内存索引。优点是召回很高，缺点是内存使用很大。

论文认为上述两个方案的局限在于它们构建的索引只能使用内存服务。

零售级的SSD一次随机读需要几百微秒，每秒能处理约300k的随机读。而搜索应用中最近邻检索的时延要求为几毫秒。因此设计高效的SSD驻留索引的关键有两点：减少随机SSD访问到几十个；减少到磁盘的round trip请求数到10个以内，最好到5个。（个人理解第一点在强调图的直径不能太大，第二点在强调减少磁盘访问，即后面提出的W参数）

2 Vamana 图构建算法

2.1 近似邻居图和GreedySearch算法

基于近似图的检索算法，一般采用贪心算法，从某个点出发，遍历图来渐近的趋向检索点。这要求近似图满足sparse neighborhood graph(SNG)的性质。SNG中确定一个点p的出邻居的过程如下：

initialize a set S = P \ {p}. As long as S != ∅, add a directed edge from p to p∗, where p∗ is the closest point to p from S, and remove from S all points p′ such that d(p, p′) > d(p∗, p′). It is then easy to see that GreedySearch(s, x_p, 1, 1) starting at any s ∈ P would converge to p for all base points p ∈ P .

大致是从S中选依次选到p最近的点p*，然后移除S中到p比到p*更远的点，直到S为空。

SNG的复杂度是O(n2)，因此不可行。本质上来说，HNSW和SSG都是对SNG的近似，因此这些算法输出的图的直径和密度都是不可灵活控制的。

2.2 健壮剪枝过程

满足SNG性质的图的直径可能非常大。论文给出的极端情况为所有点都在一条直线上，按照SSG的选边算法每个点只会连接最近的两个点。而按照Vamana的算法，有可能连接更多的点。

为了解决这个问题，引入乘数α>1要求检索路径上的点到query的距离依次减少α倍。

如果点p的出邻居通过RobustPrune(p, P \ {p}, α, n-1) 确定，可以保证GreedySearch(s, p, 1, 1) 从任意点s出发将在log复杂度内收敛到 p ∈ P。但是这需要O(n2)的运行时间。Vamana通过精心挑选V和远小于n-1的点来优化索引构建时间。

RobustPrune最后的裁边中，通过引入α，将距离p*比距离p近1/α倍的点移除掉了，可以保留更多的长边（α越大，越有可能在候选集中保留距离p更远的点）。

2.3 Vamana索引算法

  1. 首先随机初始化G，每个点有R个随机选择的出邻居。
  2. 计算数据集P的中心点s，作为检索算法的起始点。
  3. 随机遍历P的所有点p，对GreedySearch访问的点运行RobustPrune来得到点p的出邻居。
  4. 对点p的出邻居p’添加反向边p’p，如果出度超过R则运行RobustPrune来选边。

随着算法的运行，图变得一致地更好，GreedySearch运行更快。

整体算法运行两遍，第一次使用α=1运行，第二次使用用户定义的α≥1运行。作者观察到第二次运行得到更好的图，如果两次都用用户定义的α运行会使索引算法变慢，因为第一次运行计算出的图的平均度数更大，计算时间也更长。（第一次运行如果使用α>1的话，候选集中保留了更多的点，最后的度数也会更大）

第二次运行引入了长边。

2.4 对比HNSW和NSG

HNSW和NSG没有超参数α，隐含使用了α=1. 这是Vamana实现在图的度数和直径之间更好权衡的主要因素。

  • HNSW使用GreedySearch的输出作为剪枝的候选集，而Vamana和SNG都使用GreedySearch访问过的点作为候选集。直觉上来说，这帮助Vamana和NSG添加了长边，而HNSW只有邻近边还需要在采样的点上构建分层图。
  • NSG要求输入为构建耗时长和内存使用高的kNN邻居图，HNSW和Vamana有更简单的初始化，HNSW使用空白图，Vamana使用随机图。Vamana使用随机图初始化比空白图初始化得到的结果图的质量更好。
  • Vamana需要运行两遍，HNSW和NSG只需要运行一遍。

3 DiskANN：构建SSD驻留的索引

3.1 索引设计

基本思想是构建Vamana索引并存储到SSD上。有两个问题需要解决：如何构建有10亿个点的图？内存中存不下的情况下如何计算query点和候选列表的点之间的距离？

与其在检索时将query点路由到多个分片，不如将base point发往多个临近的中心点来形成重叠的聚类。

  1. 将10亿个点使用k-means划分为k个聚类（比如k=40）
  2. 将每个base point分配到l个最近的中心点（通常l=2就足够了）
  3. 在每个聚类上构建Vamana索引，大约有Nl/k个点，可以在内存中构建。
  4. 通过简单的合并边将多个图合并为一个图。

经验地，不同聚类的重叠性提供了足够的连接性，即使query点的最近的邻居分开在多个分片时GreedySearch也能成功。

解决第二个问题的思路为在内存中存储每个点的PQ压缩后的向量，同时在SSD上存储图。论文指出Vamana构建索引时使用全精度的坐标，因此即使在检索时使用压缩后的数据，也能高效的引导检索到图中正确的区域。

3.2 索引布局

内存中存储压缩后的所有数据点，SSD上存储图和全精度的向量。在磁盘上，在每个点的≤R个邻居之后存储的是全精度向量。在度数小于R时补0，以便可以直接计算offset。

基本的贪心算法的问题是需要有许多SSD roundtrip，导致高延迟。为了减少SSD roundtrip数而不过度增加计算量，我们一次获取 $\mathcal{L} \backslash \mathcal{V}$ 中W（比如4，8）个最近的点的邻居，更新$\mathcal{L}$为top L的候选集。注意从SSD读取少量的随机扇区的时间几乎和一个扇区的时间相同。修改后的检索算法称为BeamSearch。在W=1时，等价于贪心检索。如果W过大，比如16或更多，计算和SSD带宽都可能是浪费的。

SSD带宽打满时，读延迟会超过1ms。因此需要在更低的负载下运维SSD以保证低检索延迟。论文发现在低平衡宽度时（如W=2,4,8）能在延迟和吞吐之间取得平衡。这时SSD的load factor在30-40%，每个线程query处理的时间中40-50%是在IO上。

3.4 缓存频繁访问的点

为了进一步减少每个query的磁盘访问数，在内存中缓存一部分点，要么基于已知的query分布，要么简单的缓存从起始点开始C=3,4跳的点。因为点的个数随C指数增长，更大的C带来更大的内存使用。

3.5 使用全精度向量隐式Re-Ranking

PQ是有损压缩，因此使用PQ和使用真实距离计算的k个候选集可能有差别。为了消除差距，论文使用在每个点的邻居之后存储的全精度向量。邻居关系和全精度向量可以存储在同一扇区内，因此在BeamSearch加载邻居信息时，也可以缓存在搜索过程中访问过的所有点的全精度向量，而不使用额外的SSD读。这可以让我们基于全精度向量来返回top k候选集。（按上面的算法1，访问过的点都是要记录的，有额外的计算开销但没有内存开销。）

4 评估

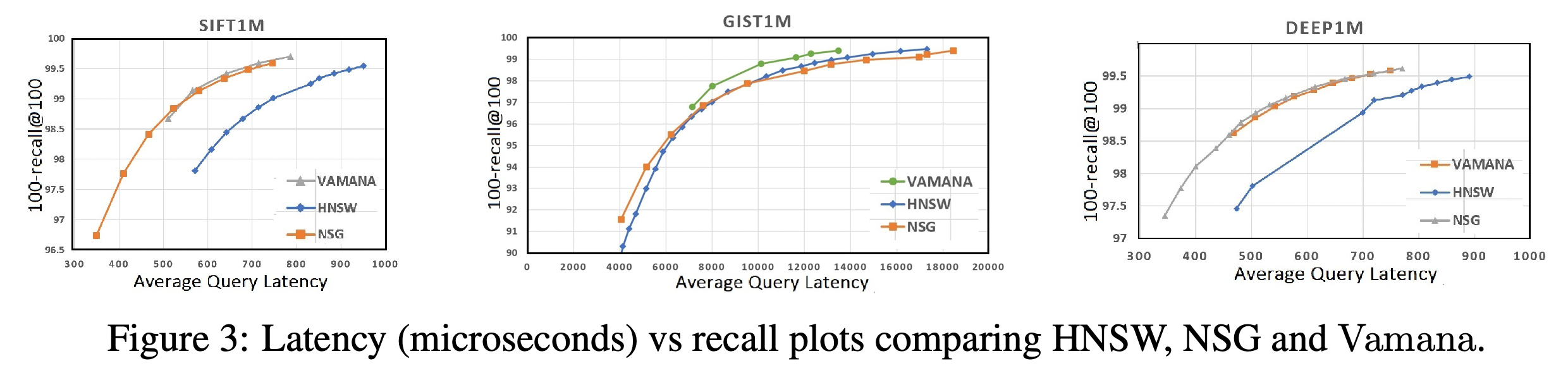
所有数据集中，Vamana超过了HNSW。在GIST1M中，Vamana超过了NSG。另外在三个实验中，Vamana的索引构建时间短于HNSW和NSG。在DEEP1M上，分别为129s, 219s, 480s（包含EFANN构建kNN图的时间）。

跳数指在检索的关键路径中磁盘访问的轮数。HNSW和NSG有停滞的趋势，而Vamana随最大度数和α的增加跳数在减少。作者推断α>1的Vamana相比其他图算法更有效的利用了SSD提供的大容量。

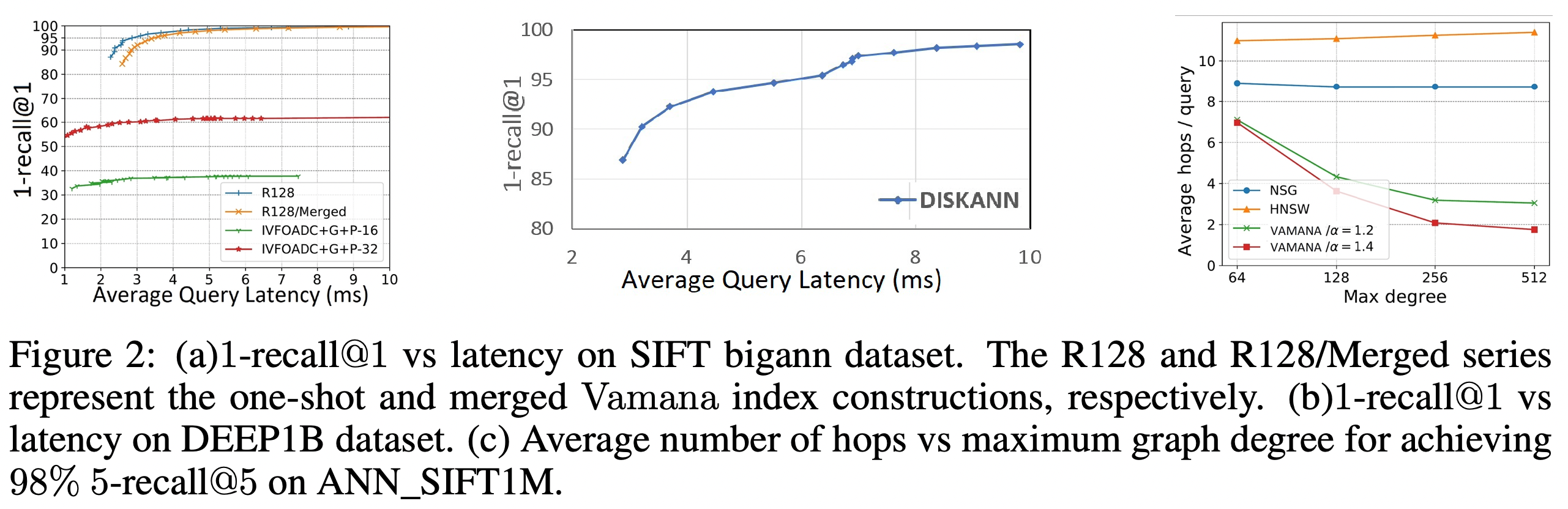
为了说明小索引合并算法的有效性，论文分别在高配机器上构建1份大索引和在低配机器上构建k份小索引并合并为1份索引。2(a)中单一索引的性能优于合并索引，因为合并索引需要遍历更多的连接。但合并索引的效果也足够好，优于当时的state-of-art IVFOADC+G+P，延时仅比单一索引慢不到20%.

由于IVFOADC+G+P在之前的论文中证明了效果优于FAISS，论文只对比了DiskANN和IVFOADC+G+P。IVFOADC+G+P的1-recall@1上限为62.74%，而DiskANN为100%，满足1-recall@1高于95%时的时延在3.5ms以下。

参考资料

审稿意见

视频

论文笔记